حل تمارين درس صيغ معادلة المستقيم - التوازي والتعامد

تأكد:

اكتب بصيغة الميل والمقطع معادلة المستقيم المعطى ميله ومقطع المحور y له في كل مما يأتي، ثم مثله بيانيا:

1) m= 4, b= -3

الحل:

معادلة المستقيم = y=mx+b --> y=4x-3

2) m= ½ ,b= -1

الحل:

معادلة المستقيم = y=mx+b --> y= ½ x – 1

3) m= -3/2, b=5

الحل:

معادلة المستقيم = y= mx + b --> y= -3/2 x +5

اكتب بصيغة الميل ونقطة معادلة المستقيم المعطى ميله ونقطة يمر بها في كل مما يأتي، ثم مثله بيانيا:

4) m= 5, (3,-2)

الحل:

y-y1 = m(x-x1) à y – (-2)=5(x – 3 ) à y+2 = 5x-15

معادلة المستقيم = y=5x-17

5) m= ¼ , (-2,-3)

الحل:

y-y1 = m(x-x1) à y – (-3) = ¼ (x – (-2))

y+3 = ¼ x + ½ à y = ¼ x + ½ -3

معادلة المستقيم = y = ¼ x – 5/2

6) m= -4.25, (-4,6)

الحل:

y – y1 = m ( x – x1) à y – 6 = -4.25( x – (-4))

y – 6 = -4.25x +4 à y = -4.25x +6 +4

معادلة المستقيم = y= -4.25x + 10

اكتب بصيغة الميل والمقطع معادلة المستقيم الذي أعطيت نقطتان يمر بهما في كل مما يأتي:

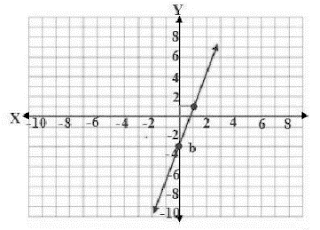
7) (0,-1),(4,4)

الحل:

8) (4,3), (1,-6)

الحل:

9) (6,5), (-1,-4)

الحل:

10) اكتب بصيغة الميل والمقطع معادلة المستقيم العمودي على y=-2x+6، والمار بالنقطة (3,2).

الحل:

ميل المستقيم y = -2x + 6 لذا ميل المستقيم العمودي عليه = ½

Y = mx + b à 2 = ½ x 3 + b

b = ½

معادلة المستقيم العمودي = y= ½ x + ½

11) اكتب بصيغة الميل والمقطع معادلة المستقيم الذي يمر بالقطة (-1,5)، ويوازي المستقيم الذي معادلته y=4x-5.

الحل:

ميل المستقيم y = 4x – 5 --> 4 لذا ميل المستقيم الذي يوازيه = 4

y = mx + b --> 5 = -1 x 4 +b

b = 9

معادلة المستقيم العمودي = y = 4x + 9

12) عروض: يقارن سلمان بين عرضين مقدمين من ناد رياضي. يدفع بموجب العرض الأول اشتراكا شهريا قدره 100 ريال، بالإضافة إلى 10 ريالات عن كل زيارة. ويدفع بموجب العرض الثاني اشتراكا شهريا قدره 150 ريالا، ويسمح له بعشر زيارات شهريا.

a) اكتب معادلة تمثل التكلفة الشهرية لكل من العرضين.

b) مثل كلتا المعادلتين بيانيا.

c) إذا كان سلمان يريد الذهاب إلى النادي 7 مرات شهريا، فهل يشترك في العرض الأول أم الثاني؟ فسر إجابتك.

الحل:

a) معادلة العرض الأول: 10x +150 = y

معادلة العرض الثاني: 150 = y

c) العرض الثاني أفضل، حيث التكلفة 150 ريالا، على حين أن تكلفة العرض الأول 7 × 10 + 100 = 170 ريالا.

تدرب وحل المسائل:

اكتب بصيغة الميل والمقطع معادلة المستقيم المعطى ميله ومقطع المحور y له في كل مما يأتي، ثم مثله بيانيا:

13) m=-5, b=-2

الحل:

y = mx + b à y = -5x – 2

14) m=-7, b=-4

الحل:

y = mx + b à y = -7x – 4

15) m=9, b=2

الحل:

y = mx + b à y = 9x +2

16) m=12, b=4/5

الحل:

y = mx + b à y = 12x + 4/5

17) m= -3/4, (0,4)

الحل:

y = mx + b à y = -3/4 x + 4

18) m=5/11 , (0,-3)

الحل:

y = mx + b à y = 5/11 x – 3

اكتب بصيغة الميل ونقطة معادلة المستقيم المعطى ميله ونقطة يمر بها في كل مما يأتي، ثم مثله بيانيا:

19) m=2, (3,11)

الحل:

y – y1 = m(x-x1) à y – 11 = 2(x-3)

y – 11 = 2x – 6

y = 2x – 6 +11

معادلة المستقيم = y =2x + 5

20) m=4, (-4,8)

الحل:

y – y1 = m(x – x1) à y – 8 = 4(x – (-4))

y – 8 = 4x + 16

معادلة المستقيم = y = 4x + 24

21) m=-7, (1,9)

الحل:

y – y1 = m(x – x1) à y – 9 = -7(x – 1)

y – 9 = 7x + 7

y = -7x +7 +9

معادلة المستقيم = y = -7x +16

22) m=5/7, (-2,-5)

الحل:

23) m=-4/5, (-3,-6)

الحل:

24) m=-2.4,(14,-12)

الحل:

اكتب بصيغة الميل والمقطع معادلة المستقيم الذي أعطيت نقطتان يمر بهما في كل مما يأتي:

25) (-1, -4), (3,-4)

الحل:

26) (2.-1), (2,6)

الحل:

27) (-3,-2), (-3,4)

الحل:

28) (0,5), (3,3)

الحل:

29) (-12,-6),(8,9)

الحل:

30) (2,4), (-4,-11)

الحل:

اكتب بصيغة الميل والمقطع معادلة المستقيم الممثل بيانيا، أو المعطى وصفه في كل مما يأتي:

31) EF

الحل:

32) MN

الحل:

33) يحوي النقطتين (-1,-2),(3, 4)

الحل:

34) يحوي النقطتين (-4, -5), (-8,-13).

الحل:

35) مقطع المحور x يساوي 3، ومقطع المحور y يساوي -2

الحل:

36) مقطع المحور x يساوي – ½ ، ومقطع المحور y يساوي 4.

الحل:

اكتب بصيغة الميل والمقطع معادلة المستقيم الذي يحقق المعطيات في كل مما يأتي:

37) يمر بالنقطة (-7, -4)، ويعامد المستقيم y= ½ x+9.

الحل:

38) يمر بالنقطة (-1,-10)، ويوازي المستقيم y=7.

الحل:

39) يمر بالنقطة (6,2)، ويوازي المستقيم y=-2/3 x+1.

الحل:

40) يمر بالنقطة (-2,2)، ويعامد المستقيم y=-5x -8.

الحل:

41) جمعية خيرية: نظمت جمعية خيرية حفلا لتكريم مجموعة من حفظة القرآن الكريم، فاستأجرت قاعة لتقيم فيها الحفل. إذا كانت أجرة القاعة 1500 ريال بالإضافة إلى 15.5 ريالا عن كل شخص يحضر الحفل.

a) اكتب معادلة تمثل تكلفة استئجار القاعة y إذا حضر x شخصا.

b) مثل المعادلة بيانيا.

c) إذا حضر الحفل 285 شخصا، فكم تكون تكلفة استئجار القاعة؟

d) إذا رصدت الجمعية 6000 ريالا لاستئجار القاعة، فما عدد الأشخاص الذين يمكن أن يحضروا الحفل؟

الحل:

a) y= 15.5x + 1500

c) y = 15.5 x + 1500

y = 15.5(285) + 1500

y = 5917.5

d) y = 15.5 x + 1500

6000 = 15.5 x + 1500

15.5 x = 6000 – 1500

15.5 x = 4500

x = 290

42) توفير: يوفر عبد الله نقودا ليشتري مذياعا مرتبطا بالأقمار الاصطناعية، ويدفع رسوم الاشتراك السنوي بخدمة الأقمار الاصطناعية. فبدأ بتوفير 200 ريال أهديت إليه في عيد الأضحى، وبعد ذلك كان يضيف 40 ريالا كل أسبوع.

a) اكتب معادلة تمثل ما وفره عبد الله y بعد x أسبوعا.

b) مثل المعادلة بيانيا.

c) متى يوفر 500 ريال؟

d) إذا بدأ التوفير منذ أسبوعين، وكان ثمن المذياع 700 ريال، ورسم الاشتراك السنوي بخدمة الأقمار الاصطناعية 420 ريالا، فمتى يوفر مبلغا يكفي لذلك؟ فسر إجابتك.

الحل:

a) y = 40 x + 200

بعد 8 أسابيع يستطيع أن يوفر 500 ريال

d) واحد و عشرون (21) أسبوع ، إذا بدأ عبد الله التوفير قبل أسبوعين، فسيكون لديه 200 ريال + 40 ريال + 40 ريال أو 280 ريالا. وبما أنه يحتاج إلى توفير 240 + 700 أو 1120 ريالا. فهو ما زال في حاجة إلى 280 – 1120 أو 840 ريالا، وبقسمة 840 ريالا على 40 ريالا، سيحتاج سلطان إلى 21 أسبوعا زيادة حتى يوفر نقود كافية.

استعمل الشكل المجاور لتسمي أي مستقيم يحقق الوصف في كل مما يأتي:

43) يوازي المستقيم y=2x – 3.

الحل:

44) يعامد المستقيم y= ½ x+7.

الحل:

45) يتقاطع مع المستقيم y= ½ x – 5، ولكنه لا يعامده.

الحل:

N أو p أو r.

حدد ما إذا كان المستقيمان متوازيين أو متعامدين، أو غير ذلك في كل مما يأتي:

46) Y=2x+4, y=2x – 10.

الحل:

متوازيان لأن ميل كل منهما متساوي ويساوي 2.

47) Y= - ½ x – 12, y= 2x+7.

الحل:

متعامدان لأن حاصل ضرب ميل كل منهما يساوي -1

48) Y – 4 = 3(x+5), y+3 = - 1/3(x+1)

الحل:

متعامدان لأن حاصل ضرب ميل كل منهما يساوي -1

49) Y – 3 = 6(x+2), y+3= - 1/3(x – 4)

الحل:

غير ذلك لأن ميل كل منهما غير متساوي وليس حاصل ضربهما = -1.

50) اكتب بصيغة الميل والمقطع معادلة المستقيم الذي يمر بالنقطة (4,2) ويوازي المستقيم y – 2 = 3(x+7).

الحل:

51) اكتب معادلة المستقيم الذي يمر بالنقطة (-8, 12) ويعامد المستقيم الذي يمر بالنقطتين (3.2),(-7,2).

الحل:

52) صناعة الفخار: نظمت جمعية حرف يدوية دورة في صناعة الفخار، وكان رسم الاشتراك 150 ريالا، بحيث يغطي اللوازم والمواد وكيسا واحدا من طين الصلصال. وكل كيس إضافي يكلف 40 ريالا. اكتب معادلة تمثل تكلفة الاشتراك وعدد x من الأكياس المستعملة.

الحل:

53) تمثيلات متعددة: طلب مدير قصر أفراح من بسام أن ينظم وقوف السيارات في أثناء حفل. وقدم له عرضين للأجر، أحدهما أن يدفع له 4 ريالات عن كل سيارة، والآخر أن يعطيه أجرا مقداره 150 ريالا بالإضافة إلى ريالين عن كل سيارة.

a) جدوليا: أنشئ جدولا يبين ما يتقاضاه بسام عن 20، 50، 100 سيارة في كلا العرضين.

b) عدديا: اكتب معادلة تمثل ما يكسبه بسام من كل عرض.

c) بيانيا: مثل بيانيا كلا من معادلتي العرضين.

d) تحليليا: أي العرضين أكثر كسبا لباسم، إذا كان عدد السيارات 35 سيارة؟ وأيهما أكثر كسبا إذا كان عدد السيارات 80 سيارة؟ وضح إجابتك.

e) لفظيا: اكتب عبارة تصف العرض الأكثر كسبا لبسام تبعا لعدد السيارات.

f) منطقيا: إذا كان عدد السيارات 75 سيارة، فأي العرضين أكثر كسبا لباسم؟ وضح تبريرك.

الحل:

b) y = 4x

y = 2x + 150

d) إذا كان عدد السيارات 35، فإنه يكسب 140 ريالا من العرض الأول و 150 + 2(35) أو 220 ريالا من العرض الثاني، إذن فالعرض الثاني أفضل.

إذا كان عدد السيارات 80 سيارة، فإنه يكسب 320 ريالا مع العرض الأول، ويكسب 310 ريالات أكثر من 75 سيارة فإن العرض الأول أكثر كسبا.

e) إذا كان عدد السيارات اقل من 75 سيارة فإذن العرض الثاني أكثر كسبا، وإذا كان عدد السيارات أكثر من 75 سيارة فإن العرض الأول أكثر كسبا.

f) إذا كان عدد السيارات 75 سيارة:

150 + 2(75) = 150 + 150 = 300 العرض الأول.

4(75) = 300 العرض الثاني

العرض الأول والثاني متساويان.

مسائل مهارات التفكير العليا:

54) تحد: أوجد قيمة n، بحيث يمر المستقيم العمودي على المستقيم -2y+4 =6x+8 بالنقطتين (n,-4), (2,-8).

الحل:

55) تبرير: حدد ما إذا كانت النقاط (-2,2), (2,5), (6,8) تقع على استقامة واحدة. برر إجابتك.

الحل:

56) مسألة مفتوحة: اكتب معادلات زوجين مختلفين من المستقيمات المتعامدة التي تتقاطع في النقطة (-3, -7).

الحل:

X = -3

Y = -7

57) اكتشف الخطأ: كتب كل من ركان وفيصل معادلة مستقيم ميله -5، ويمر بالنقطة (-2.4)، أيهما إجابته صحيحة؟ وضح تبريرك.

الحل:

الحلان صحيحان، كتب فيصل المعادلة بصيغة الميل والمقطع، في حين كتبها ركان بصيغة الميل ونقطة.

58) اكتب: أيهما أسهل كتابة: معادلة مستقيم بصيغة الميل ونقطة، أم بصيغة الميل والمقطع؟

الحل:

إذا أعطيت الميل ومقطع المحور y يكون استعمال صيغة الميل والمقطع أسهل، وعندما تعطى نقطتين أو الميل ونقطة يكون استعمال صيغة الميل ونقطة أسهل.

تدرب على اختبار:

59) أي مما يأتي هو التمثيل البياني للمستقيم الذي يمر بالنقطة (-2, -3)؟

الحل:

60) أي مما يأتي هي معادلة المستقيم الذي يمر بالنقطة (-2,1)، ويعامد المستقيم y = 1/3 x + 5؟

A. Y=3x+7

B. Y=1/3x+7

C. Y=-3x-5

D. Y=-1/3x-5

الحل:

طريقة الحل:

مراجعة تراكمية

أوجد ميل المستقيم الذي يمر بالنقطتين A,B في كل ما يأتي:

61) A(4,3), B(5,-2)

الحل:

62) A(0,2), B(-3,-4)

الحل:

63) A(2,5), B(5,1)

الحل:

أوجد قيمة x, y في كل من الشكلين الآتيين:

64)

الحل:

65)

الحل:

في الشكل المجاور: m<1 = 58 , m<2= 47 , m<3 = 26. أوجد قياس كل من الزوايا الآتية:

66) <7.

الحل:

<7 = <1 = 58 نظرية الزاويتان المتناظرتان متساويتان.

67) .<5

الحل:

<5 = <2 = 47 نظرية الزاويتان المتبادلتان متساويتان.

68) <6.

الحل:

<6 = <1 + <2 – 180 = 75 لأن مجموع زوايا المثلث الداخلية 180.

69) <4.

الحل:

<4 = <3 + <5 – 180 = 107 لأن مجموع زوايا المثلث الداخلية 180.

70) <8.

الحل:

<8 = <3 + <2 = 26 + 47 = 73 نظرية الزاويتان المتناظرتان متساويتان.

71) <9.

الحل:

<9 = <8 + <7 – 180 = 73 + 58 – 180 = 49 لأن مجموع زوايا المثلث الداخلية 180.

استعد للدرس اللاحق

72) إذا كان BE , AD متعامدين، فأوجد قيمة كل من x, y

الحل:

متبادلتان خارجيا.

جديد

العلم نور

الأحد، 2 مايو 2021

حل تمارين درس صيغ معادلة المستقيم - التوازي والتعامد